What is Elliptic Curve Cryptography (ECC)?

Elliptic Curve Cryptography (ECC) is a powerful and efficient approach to public-key cryptography, offering robust security with smaller key sizes compared to traditional methods. This article will provide you with a clear understanding of ECC, its benefits, and its applications in modern cybersecurity.

Quick Overview

• ECC is a public-key cryptography system based on the algebraic structure of elliptic curves over finite fields.
• It provides equivalent security to RSA with much shorter key lengths, resulting in faster computations and lower resource usage.
• ECC is widely used in various applications, including secure communication, digital signatures, and cryptocurrency.

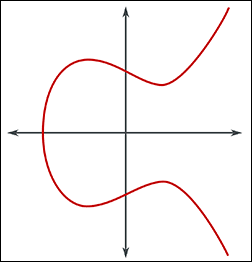
What is an Elliptic Curve?

An elliptic curve is a mathematical curve defined by the equation:

y² = x³ + ax + b

Where a and b are constants. In cryptography, we use elliptic curves over finite fields, which means the x and y coordinates are limited to a specific range of integers.

Key properties of elliptic curves:

• Symmetric about the x-axis
• Non-singular (no cusps or self-intersections)
• The curve intersects each vertical line in at most three points

Applications of ECC

1. Secure Communication: Used in protocols like TLS/SSL for encrypted web communication.
2. Digital Signatures: Employed in various digital signature schemes, such as ECDSA (Elliptic Curve Digital Signature Algorithm).
3. Cryptocurrency: Many cryptocurrencies, including Bitcoin and Ethereum, use ECC for key generation and digital signatures.
4. Mobile Devices: ECC’s efficiency makes it ideal for resource-constrained mobile devices.
5. Internet of Things (IoT): Used in securing communication between IoT devices with limited processing power and memory.
6. Government and Military: Adopted by the NSA for protecting classified information.

How ECC Works

ECC leverages the mathematical properties of elliptic curves to create secure cryptographic systems. Here’s a simplified explanation of the process:

1. Choose an elliptic curve and a point on the curve as the generator point (G).
2. Select a private key (a random integer).
3. Multiply the generator point by the private key to obtain the public key.
4. Use the public key for encryption or signature verification.

The security of ECC relies on the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP), which involves finding the scalar value used to multiply a point on the curve.

Advantages of ECC

• Smaller Key Sizes: ECC provides equivalent security to RSA with significantly smaller key sizes. For example, a 256-bit ECC key offers comparable security to a 3072-bit RSA key.
• Faster Computations: Smaller key sizes lead to faster computations, making ECC more efficient for resource-constrained devices.
• Lower Resource Usage: ECC requires less memory and bandwidth, making it ideal for mobile devices and IoT applications.
• Future-Proof: As computing power increases, ECC scales more efficiently than RSA, requiring smaller increases in key size to maintain security.

ECC vs. RSA: A Comparison

Elliptic Curve Cryptography (ECC) and RSA are two widely used public-key cryptographic methods. While RSA has been a standard for many years, ECC offers comparable security with smaller key sizes, making it more efficient for modern applications. The following comparison outlines key differences between the two.

Security Level (bits)	ECC Key Size	RSA Key Size
80	160	1024
112	224	2048
128	256	3072
192	384	7680
256	521	15360

As the table demonstrates, ECC provides the same level of security as RSA but with significantly smaller key sizes. This reduction in size leads to faster performance and lower resource consumption, making ECC ideal for devices with limited computing power.

Popular ECC Curves

Several standardized elliptic curves are widely used in cryptographic applications:

• NIST Curves: Developed by the US National Institute of Standards and Technology (NIST), including P-256, P-384, and P-521.
• Curve25519: Designed for use with the Elliptic Curve Diffie-Hellman (ECDH) key agreement scheme.
• secp256k1: Used in Bitcoin and other cryptocurrencies.
• Brainpool Curves: A set of ECC curves developed by the Brainpool consortium, offering an alternative to NIST curves.

Implementing ECC: Best Practices

When implementing ECC in your systems, consider the following best practices:

1. Choose Appropriate Curves: Select well-vetted, standardized curves appropriate for your security requirements.
2. Use Secure Random Number Generators: Ensure that private keys are generated using cryptographically secure random number generators.
3. Implement Proper Key Management: Securely store and manage private keys, and have a process for key rotation.
4. Validate Public Keys: Always validate received public keys to ensure they are valid points on the chosen elliptic curve.
5. Stay Updated: Keep your ECC implementations up-to-date with the latest security patches and recommendations.
6. Consider Side-Channel Attacks: Implement countermeasures against side-channel attacks, such as timing attacks or power analysis.

Challenges and Limitations of ECC

While ECC offers significant advantages, it’s important to be aware of its challenges and limitations:

• Patent Issues: Some ECC algorithms were patented, which initially slowed adoption. However, many key patents have now expired.
• Implementation Complexity: Correct implementation of ECC can be more complex than RSA, requiring careful attention to detail.
• Quantum Computing Threat: Like other public-key cryptosystems, ECC is vulnerable to attacks by large-scale quantum computers (although less so than RSA).
• Limited Adoption: Despite its benefits, ECC is not as widely adopted as RSA in some areas, which can lead to compatibility issues.

The Future of ECC

The efficiency and security of ECC make it a crucial technology for the future of cryptography. Here are some trends to watch:

• Post-Quantum Cryptography: Research is ongoing to develop ECC-based systems resistant to quantum computer attacks.
• Increased Adoption: As the benefits of ECC become more widely recognized, we can expect increased adoption across various industries.
• Standardization: Continued efforts to standardize ECC implementations and curves will improve interoperability and security.
• Integration with Emerging Technologies: ECC is likely to play a significant role in securing emerging technologies like 5G networks, autonomous vehicles, and advanced IoT systems.

Conclusion

Elliptic Curve Cryptography (ECC) is a powerful public-key system offering strong security with smaller key sizes compared to older methods like RSA. Its faster computations and low resource demands make it ideal for mobile devices, IoT, and secure web communications. ECC is widely used in digital signatures, cryptocurrencies, and secure online systems. As technology advances, ECC’s efficiency makes it essential for future cybersecurity.

To explore how ECC can strengthen your security, consider SSL.com’s S/MIME certificates for secure email communication and client authentication, or contact our team of experts for personalized advice via our online chat or sales@ssl.com.